Intersection of a polyhedron with a line
In computational geometry, the intersection of a polyhedron with a line is the problem of computing the intersection of a convex polyhedron and a ray in Euclidean space. This problem has important applications in computer graphics, optimization, and even in some Monte Carlo methods.
Statement of the problem
In general, a convex polyhedron is defined as the intersection of a finite number of halfspaces. That is, a convex polyhedron is the set of solutions of a system of inequations of the form
The formal statement of our problem is to find the intersection of the set 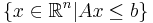 with the line defined by
with the line defined by 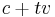 , where
, where 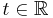 and
and 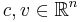 .
.
General solution
To this end, we would like to find  such that
such that 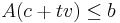 , which is equivalent to finding a
, which is equivalent to finding a  such that
such that
for 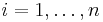 .
.
Thus, we can bound  as follows:
as follows:
The last two lines follow from the cases when the direction vector  is parallel to the halfplane defined by the
is parallel to the halfplane defined by the 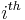 row of
row of  :
: 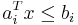 . In the second to last case, the point
. In the second to last case, the point  is on the inside of the halfspace; in the last case, the point
is on the inside of the halfspace; in the last case, the point  is on the outside of the halfspace, and so
is on the outside of the halfspace, and so  will always be infeasible.
will always be infeasible.
As such, we can find  as all points in the region (so long as we do not have the fourth case from above)
as all points in the region (so long as we do not have the fourth case from above)
which will be empty if there is no intersection.
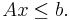
![[Av]_it \leq [b-Ac]_i](/2012-wikipedia_en_all_nopic_01_2012/I/c2965c4f768ef3c79e2b389943867094.png)
![t \leq \frac{[b-Ac]_i}{[Av]_i} \;\;\;{\rm if}\;[Av]_i > 0](/2012-wikipedia_en_all_nopic_01_2012/I/8add3cb29508c98aa0819c42eb18082f.png)
![t \geq \frac{[b-Ac]_i}{[Av]_i} \;\;\;{\rm if}\;[Av]_i < 0](/2012-wikipedia_en_all_nopic_01_2012/I/8d3910d172d70186555e407ce521577c.png)
![t {\rm\; unbounded} \;\;\;{\rm if}\;[Av]_i = 0, [b-Ac]_i > 0](/2012-wikipedia_en_all_nopic_01_2012/I/61d85db02557aec4d1590959fddfbb1d.png)
![t {\rm\; infeasible} \;\;\;{\rm if}\;[Av]_i = 0, [b-Ac]_i < 0](/2012-wikipedia_en_all_nopic_01_2012/I/d3a1bcb90c2f62172ca8458e17bddcb3.png)
![\left[ \max_{i:[Av]_i\leq 0}\frac{[b-Ac]_i}{[Av]_i}, \min_{i:[Av]_i\geq 0}\frac{[b-Ac]_i}{[Av]_i}\right],](/2012-wikipedia_en_all_nopic_01_2012/I/091483ec9b3edadf83f3658a9de3f6ea.png)